次の問いに答えなさい。
(1)9-(-5)
(2)(-3)²÷1/6
(3)√2×√14
円筒の中に1から9までの数字が1つずつ書かれた9本のくじがあります。円筒の中から1本のくじを取り出し、くじに書かれた数が偶数のとき教室清掃の担当に,奇数のとき廊下清掃の担当に決まるものとします。Aさんが9本のくじの中から1本を取り出すとき、A さんが教室清掃の担当に決まる確率を求めなさい。
次の表は、ある一次関数について、xの値とyの値の関係を示したものです。表の空欄にあてはまる数を書きなさい。
| x | … | -1 | 0 | … | 3 | … |
| y | … | 6 | … | 2 | … |
底面の半径が6cm、体積が132π㎤の円錐があります。この円錐の高さを求めなさい。
x²-□x+14が(x-a)(x-b)の形に因数分解できるとき、□に当てはまる自然数を2つ書きなさい。ただし、a,bはいずれも自然数とします。
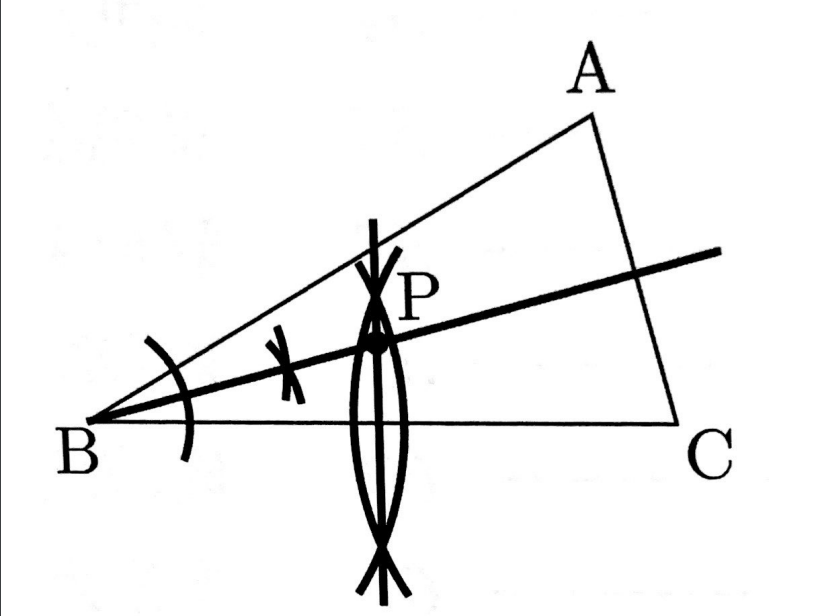
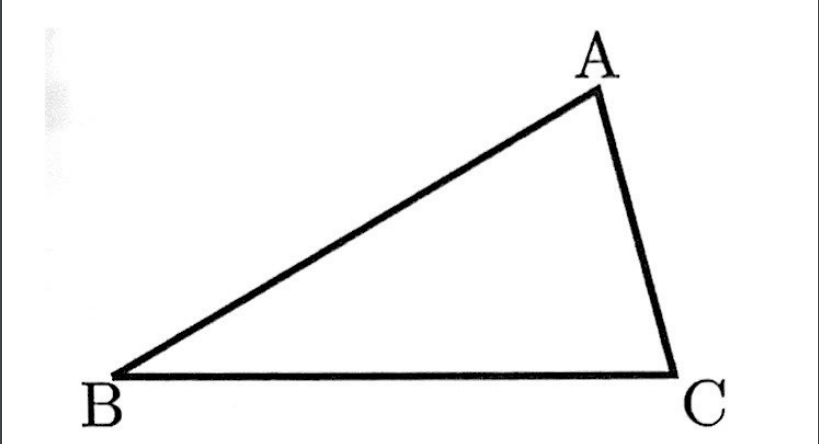
図のように∠ACB=75°、BA=BCの二等辺三角形ABCがあります。△ABCの内部に点Pをとり、∠PBC=∠PCB=15°となるようにします。点Pを定規とコンパスを使って作図しなさい。
ただし、点を示す記号Pを書き入れ、作図に用いた線は消さないこと。
(1)9-(-5)
=9+5=14
(2)(-3)²÷1/6
=9×6=54
(3)√2×√14
=√2×√(2×7)=2√7
偶数のとき教室清掃の担当になるので、1~9の中で偶数は「2,4,6,8」の4つ。
よって、確率は4/9
一次関数の一般式y=ax+bの式に分かっている2点(x,y)=(-1,6)(3,2)を代入して、連立方程式を解いて、a,bの値を計算するとa=-1,b=5となる。
よって、一次関数の式がy=-x+5となるので、x=0を代入すると、求めたい空欄の値は5だと分かる。
円錐の体積は「底面積×高さ÷3」で求めることができる。
円錐の高さをhとすると、
6×6×π×h÷3=132π
12πh=132π
h=11(cm)とわかる。
(x-a)(x-b)=x²-(a+b)x+abから、ab=14となるa,bの組み合わせを考えると、
(a,b)=(1,14)(2,7)(7,2)(14,1)の4通りが考えられる。よって、(a+b)=9,15が答えとなる。