2023年度公立高校入試過去問解説【北海道・数学・大問3】

テーマ：関数とグラフ

問題文

図のように、2つの関数y=ax²(aは正の定数)…①、y=-3x²…②のグラフがあります。①のグラフ上に点Aがあり、点Aのx座標を正の数とします。点Aを通り、x軸に平行な直線と①のグラフとの交点をBとします。点Oは原点とします。

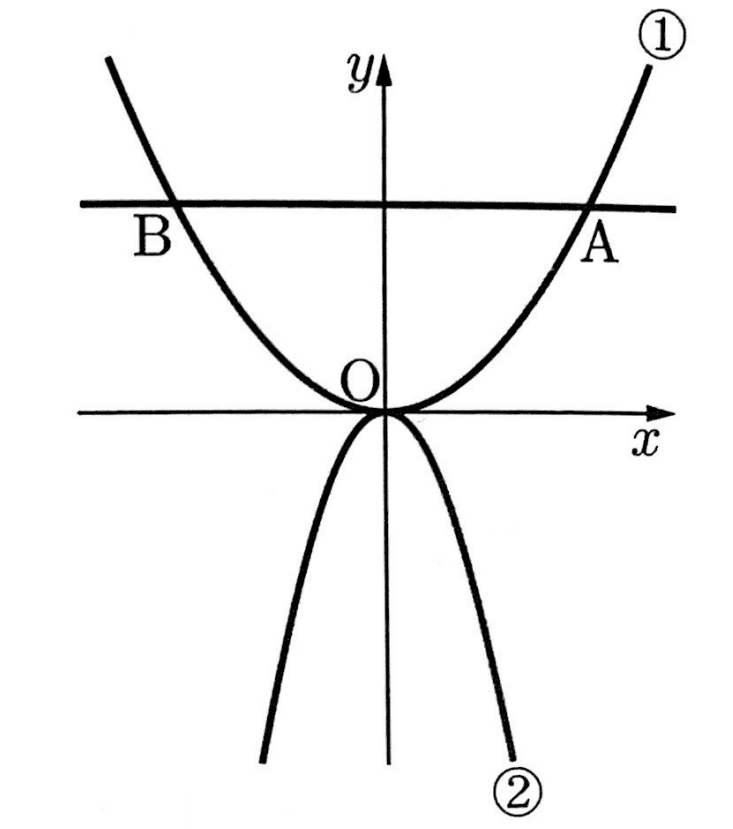
次の問いに答えなさい。

問1　

a=2とします。点Aのy座標が8のとき、点Aと点Bの距離を求めなさい。

問2　

①についてxの値が1から3まで増加するときの変化の割合が、一次関数y=x+2についてxの値が-1から2まで増加するときの変化の割合に等しいとき、aの値を求めなさい。途中の計算も書きなさい。

問3

a=1/3とします。点Aのx座標を3とします。②のグラフ上に点Cを、x軸に平行な直線と②のグラフとの交点をDとします。線分AB,CD上にそれぞれ点P,Qをとり、点Pのx座標をtとします。ただし、0<t≦1とします。
陸さんは、コンピュータを使って直線PQを動かしたところ、直線PQが原点Oを通るとき、台形ABDCの面積を２等分することに気づきました。
直線PQが原点Oを通るとき、次の（1）（2）に答えなさい。

（1）点Qの座標を、tを使って表しなさい。
（2）直線PQが台形ABDCの面積を2等分することを説明しなさい。

解答・解説

問1

4
点Aの座標はy=8を①に代入し、点A(2,8)と分かる。同時に点Bの座標もわかり、点B(-2,8)である。
よって、距離は4

問2

$a=\frac{1}{4}$
変化の割合は「$\frac{yの増加量}{xの増加量}$」で求めることができる。また、変化の割合と傾きは同じことであることに注目すると、$\frac{(9a-a)}{(3-1)}=1$が立式できる。

問3

（1）点Q(-t,-3)　（2）解答以下
線分PQの中点が原点Oになるので、点Q(-t,-3)となる。
台形PQCAの面積は${(3-t)+(t+1)}\times6\times\frac{1}{2}=12$となります。…①
台形ABDCの面積は$(6+2)\times6\times\frac{1}{2}=24$となります。…②
①、②より台形PQCAの面積は台形ABDCの面積の半分なので、直線PQは台形ABDCの面積を２等分する。