

次の(1),(2)に答えなさい。
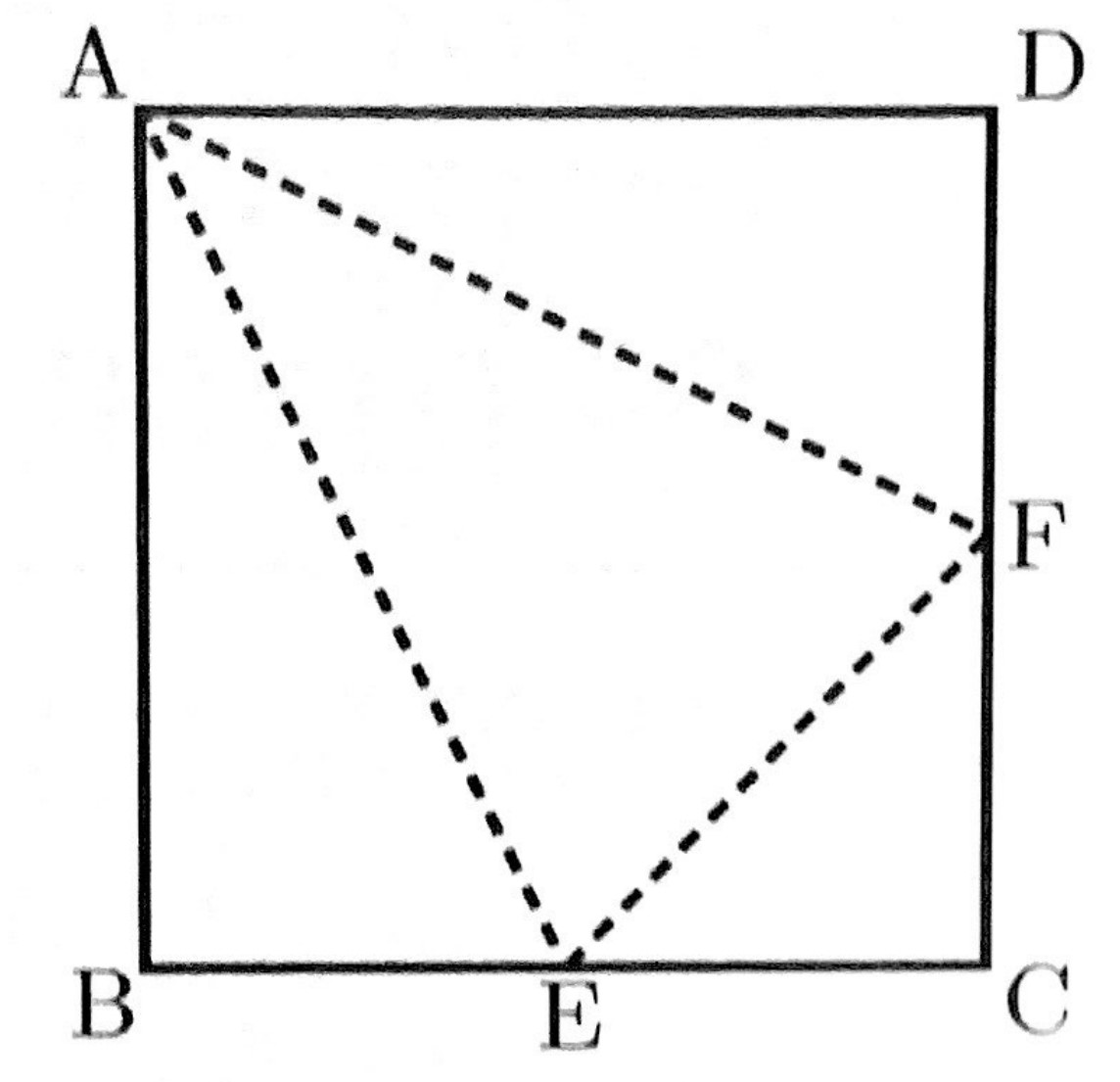
1辺の長さが8cmの正方形の紙ABCDがある。次の図は、辺BC、CDの中点をそれぞれE,Fとし、線分AE,EF,FAで折ってできる三角錐の展開図である。
次のア、イに答えなさい。
ア:線分AEの長さを求めなさい。
イ:折ってできる三角錐について、次の(ア)、(イ)に答えなさい。
(ア)体積を求めなさい。
(イ)△AEFを底面としたときの高さを求めなさい。
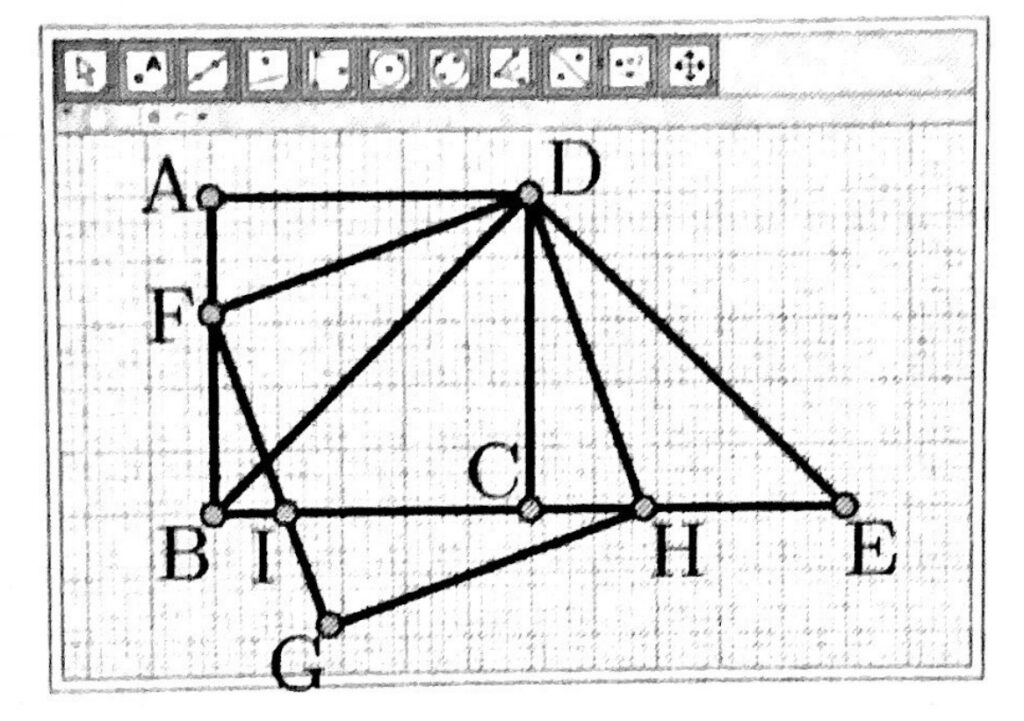
次の図のように、作図ソフトで、正方形ABCDとDB=DEの直角二等辺三角形DBEをかき、辺AB上に動く点Fを取る。また、線分DFを1辺とする正方形DFGHをかくと、点Hは辺CE上を動く点であることが分かった。辺BCと辺FGの交点をIとするとき、次のア、イに答えなさい。
△DFBと△DHEが合同になることを次のように証明した。【あ】、【い】には式、【う】には適切な内容をそれぞれ書きなさい。
【証明】
△DFBと△DHEにおいて
△DBEは二等辺三角形だから
DB=DE…①
四角形DFGHは正方形だから
【あ】…②
また、2つの直角三角形DAFとDCHにおいて
∠DAF=∠DCH=90°、DF=DH、DA=DCであるから、△DAF≡△DCH
したがって、∠ADF=∠CDHであり
∠BDF=45°-∠ADF、∠EDH=45°-∠CDHであるから
【い】…③
①、②、③から
【う】がそれぞれ等しいので
△DFB≡△DHE
AB=5cm、CH=2cmのとき、△FBIの面積を求めなさい。
ア:4√5cm
△ABEに注目すると、直角三角形になることがわかり、三平方の定理から求まる。
イ:(ア)64/3cm³
△ECFを底面とすると、ABが高さになる。
4×4×1/2×8×1/3=64/3
(イ)8/3cm
(ア)で求めた体積から逆算すれば求まる。
底面積AEFは正方形から△ABE、△ECF、△AFDの面積をそれぞれ引けば求まり
8×8-(8×4×1/2+4×4×1/2+8×4×1/2)=24cm²
高さをhとすると
24×h×1/3=64/3となるので、答えはh=8/3
ア:【あ】DF=DH 【い】∠BDF=∠EDH 【う】2組の辺とその間の角
イ:9/5cm²
△FBIの面積を求めるためには、FBとBIの長さを求めればよい。
△DAF≡△DCHより、AF=CH=2cm
よって、FB=5-2=3cm
△FBI∽△DAFより、BI:AF=FB:DA
よって、BI=2×3/5=6/5cm
求める面積は3×6/5×1/2=9/5cm²
短期間で効果を出すなら
家庭教師のひのきあすなろ!