

次の(1)~(8)に答えなさい。
ア:$4-10$
イ:$(-2)^3\times3+(-15)\div(-5)$
ウ:$(6x^2-x-5)-(2x^2+x-6)$
エ:$(6x^2y+4xy^2)\div2xy$
オ:$\sqrt{\frac{3}{2}}-\frac{\sqrt{54}}{2}$
縦がxcm、横がycmの長方形がある。このとき、2(x+y)は長方形のどんな数量を表しているか、書きなさい。
次の表は、あるクラスの生徒20人のハンドボール投げの記録を度数分布表に整理したものである。記録が20m以上24m未満の階級の相対度数を求めなさい。また、28m未満の累積相対度数を求めなさい。
| 階級(m) | 度数(人) |
| 16~20 | 4 |
| 20~24 | 6 |
| 24~28 | 1 |
| 28~32 | 7 |
| 32~36 | 2 |
| 合計 | 20 |
$3x^2-6x-45$
関数$y=ax+b$について、xの値が2増加するとyの値が4増加し、x=1のときy=-3である。このとき、a,bの値をそれぞれ求めなさい。
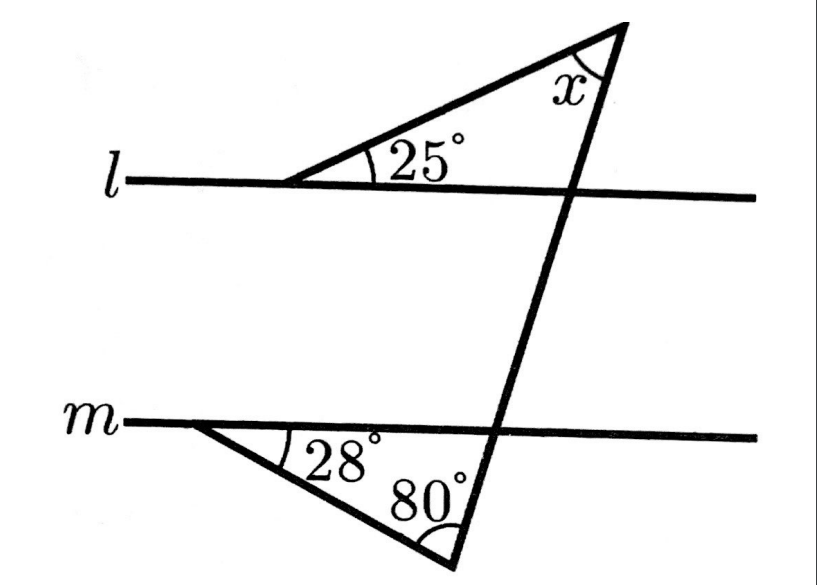
次の図で、l//mのとき、∠xの大きさを求めなさい。
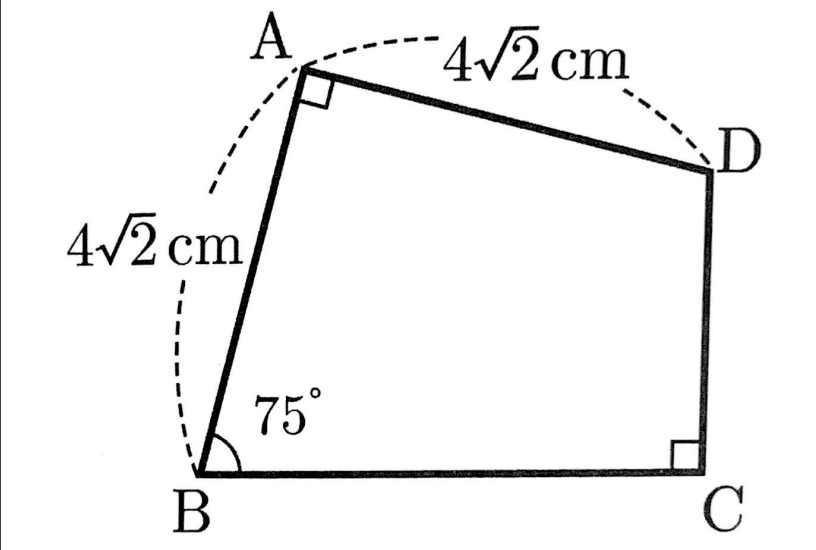
次の図で、辺BCの長さを求めなさい。
データの分布を表す値や箱ひげ図について述べた文として適切でないものを、次のア~エの中から1つ選び、その記号を書きなさい。
ア 第2四分位数と中央値は、必ず等しい。
イ データの中に極端にかけ離れた値があるとき、四分位数はその影響を受けにくい。
ウ 箱ひげ図を横向きに書いたとき、箱の横の長さは範囲(レンジ)を表している。
エ 箱ひげ図の箱で示された区間には、全体の約50%のデータが含まれる。
ア:$4-10=-6$
イ:$(-2)^3\times3+(-15)\div(-5)=12+3=15$
ウ:$(6x^2-x-5)-(2x^2+x-6)=4x^2-2x+1$
エ:$(6x^2y+4xy^2)\div2xy=3x+2y$
オ:$\sqrt{\frac{3}{2}}-\frac{\sqrt{54}}{2}=\frac{\sqrt{6}}{2}-\frac{3\sqrt{6}}{2}=-\frac{2\sqrt{6}}{2}=-\sqrt{6}$
長方形の周の長さ
相対度数は$6 \div 20=0.3$
累積相対度数は$(4+6+1) \div 20=0.55$
$3x^2-6x-45$
共通項でまとめて
=$3(x^2-2x-15)$
=$3(x-5)(x+3)$
傾きaは$\frac{yの増加量}{xの増加量}$で求まるので、$a=\frac{4}{2}=2$
さらに、x,yの値が分かっているので$y=ax+b$に代入して
$-3=2 \times 1 +b$
$b=-5$
∠x=180-(25+108)=47°
BとDを結ぶとおなじみの比の三角形($1:1:\sqrt{2}$と$1:2:\sqrt{3}$)に分かれることがポイント
$AB:BD=1:\sqrt{2}$
$4\sqrt{2}:BD=1:\sqrt{2}$
$BD=4\sqrt{2} \times \sqrt{2}=8cm$
さらに、
$BD:BC=2:\sqrt{3}$
$8:BC=2:\sqrt{3}$
$BC=8 \times \sqrt{3} \div 2=4\sqrt{3}cm$
ウ
箱の長さは四分位範囲に等しい。
短期間で効果を出すなら
家庭教師のひのきあすなろ!