

図1で、①は関数y=ax²(a>0)のグラフである。点Aは①上にあり、x座標が2である。また、点Bはx軸上にあり、x座標は点Aのx座標と同じである。次の(1),(2)に答えなさい。ただし、座標軸の単位の長さを1cmとする。
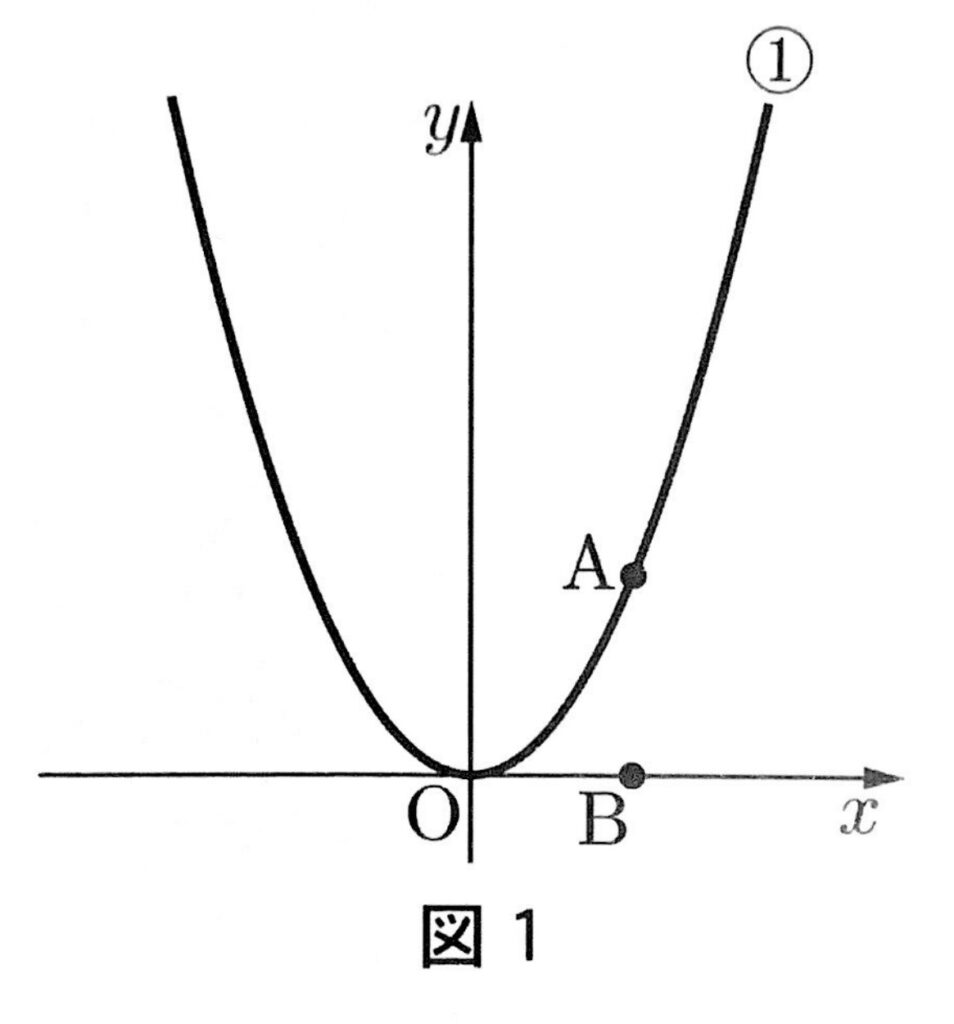
a=$\frac{1}{2}$のとき、点Aのy座標を求めなさい。
2点A,B間の距離が6cmのとき、aの値を求めなさい。
図2は、図1に正方形ABCDと△BDEを書き加えたもので、点Eは①上にあり、x座標は-1である。このとき、次のア,イに答えなさい。ただし、点Cのx座標は点Bのx座標より大きいものとする。
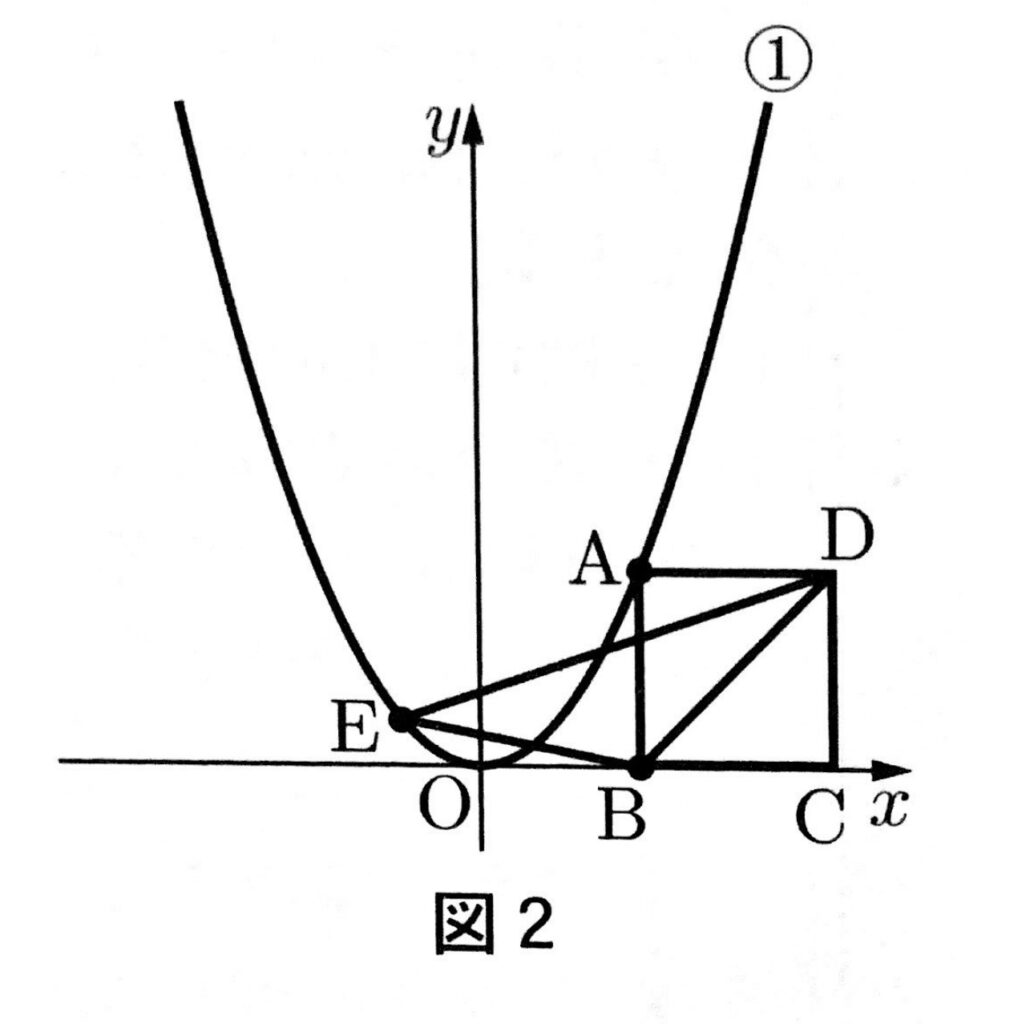
2点B,Dを通る直線の式を求めなさい。
△BDEの面積が80cm²であるとき、aの値を求めなさい。
$y=\frac{1}{2}x^2$に$x=2$を代入すればよい。
点Aの座標は$a$を用いて、$A(2,4a)$と表せる。
AB間の距離は点Aのy座標と同じなので、$4a=6$を解けばよい。
傾きは1なので、$y=x+b$に通る点$B(2,0)$を代入すればよい。
点Eからx軸に垂線EFを引くと、$EF=a,DC=AB=4a,FC=FO+OB+BC=4a+3$より
台形CDEFの面積が求まり、$10a^2+\frac{15}{2}a$
台形CDEFは△BEFと△BDEと△BCDの合計なので、$10a^2+\frac{15}{2}a=8a^2+\frac{3}{2}a+80$を解けばよい。
短期間で効果を出すなら
家庭教師のひのきあすなろ!