2023年度公立高校入試過去問解説【北海道・数学・大問2】

テーマ：数の性質

問題文

問1　

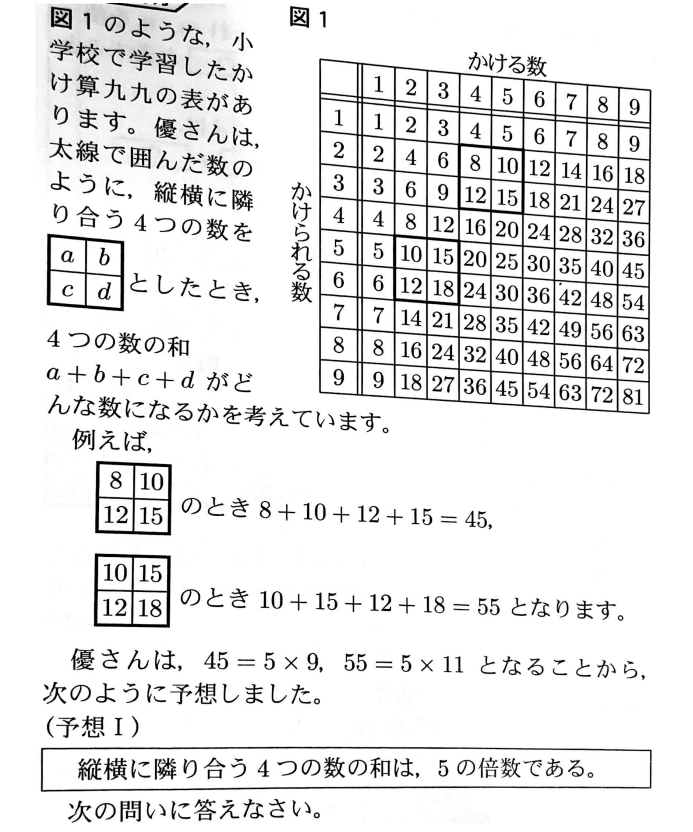
予想Ⅰが正しいとは言えないことを、次のように説明するとき、ア～オに当てはまる数を、それぞれ書きなさい。

問2　

優さんは、予想Ⅰがいつでも成り立つとは限らないことに気づき、縦横に隣り合う4つの数それぞれの、かけられる数とかける数に注目して、あらためて調べ、予想をノートにまとめました。

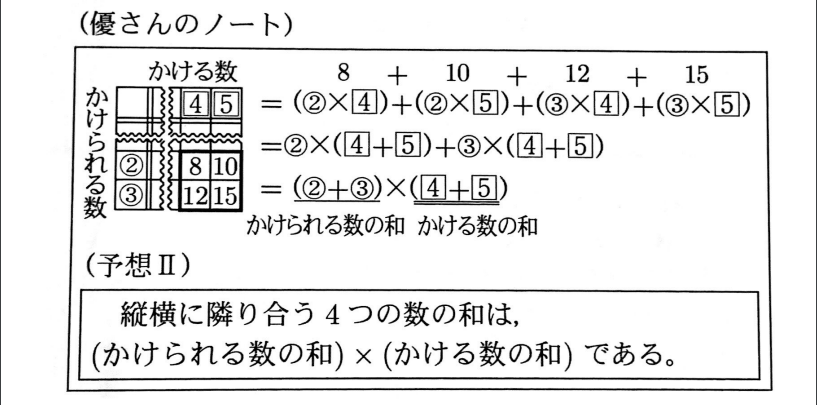
予想Ⅱがいつでも成り立つことを、次のように説明するとき、ア～キに当てはまる式を、それぞれ書きなさい。

問3

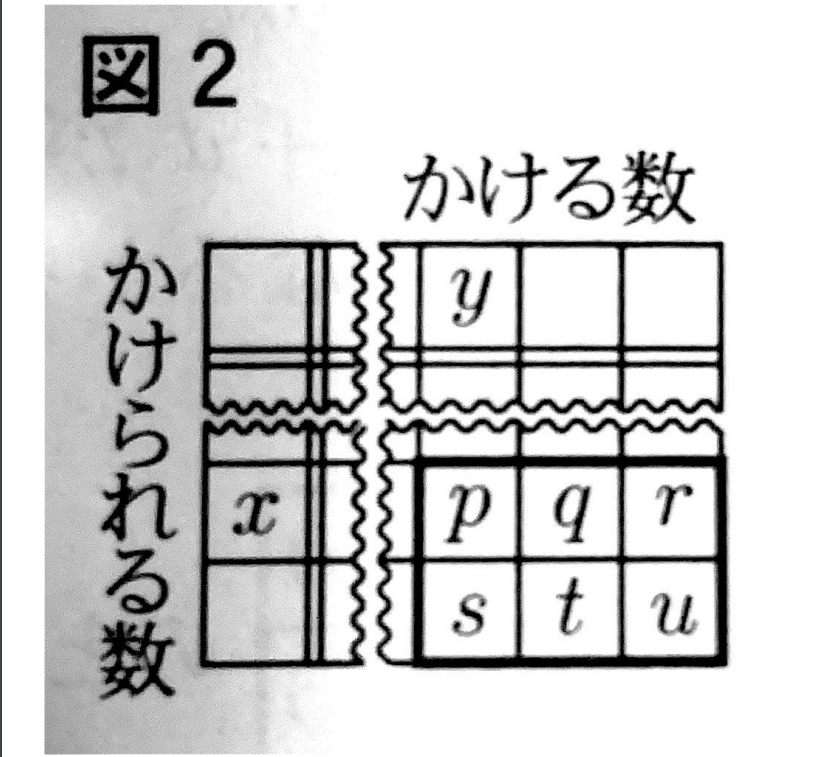
図2において，p+g+r+s+t+u＝162 となるとき，p のかけられる数x、かける数yの値を，それぞれ求めなさい。

解答・解説

問1

（ア）1　（イ）2　（ウ）2　（エ）4　（オ）9
答えは一例。反例を図1から抜き出せばよい。

問2

（ア）m(n+1)　（イ）(m+1)n　（ウ）(m+1)(n+1)　
（エ）m　（オ）m+1　（カ）n　（キ）n+1
優さんのノートを参照しながら文字式を作ればよい。

問3

x=4,y=5
設問より、{x+(x+1)}{y+(y+1)+(y+2)}=162が成り立つことがわかる。
{x+(x+1)}{y+(y+1)+(y+2)}=162
⇔(2x+1)(3y+3)=162
⇔(2x+1)(y+1)=54
54になる数字のペアは(2x+1,y+1)=(1,54)(2,17)(3,18)(6,9)(9,6)(18,3)(17,2)(54,1)
このうち、x,yが整数で、1≦x≦9,1≦y≦9を満たすのは
(9,6)のペアのみとなる。
よって、x=4,y=5