2023年度公立高校入試過去問解説【北海道・数学・大問4】

テーマ：平面図形

問題文

図のように、円Oの円周上に3点、A,B,Cをとります。∠BACの二等分線と線分BCとの交点をDとします。

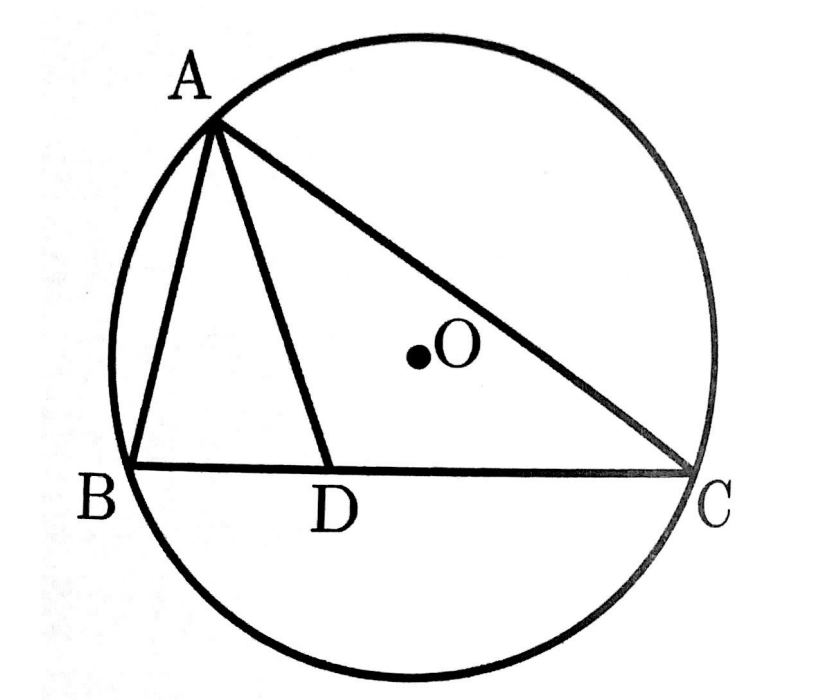
次の問いに答えなさい。

問1　

AD＝CD,∠BAD＝35°のとき、∠ADCの大きさを求めなさい。

問2　

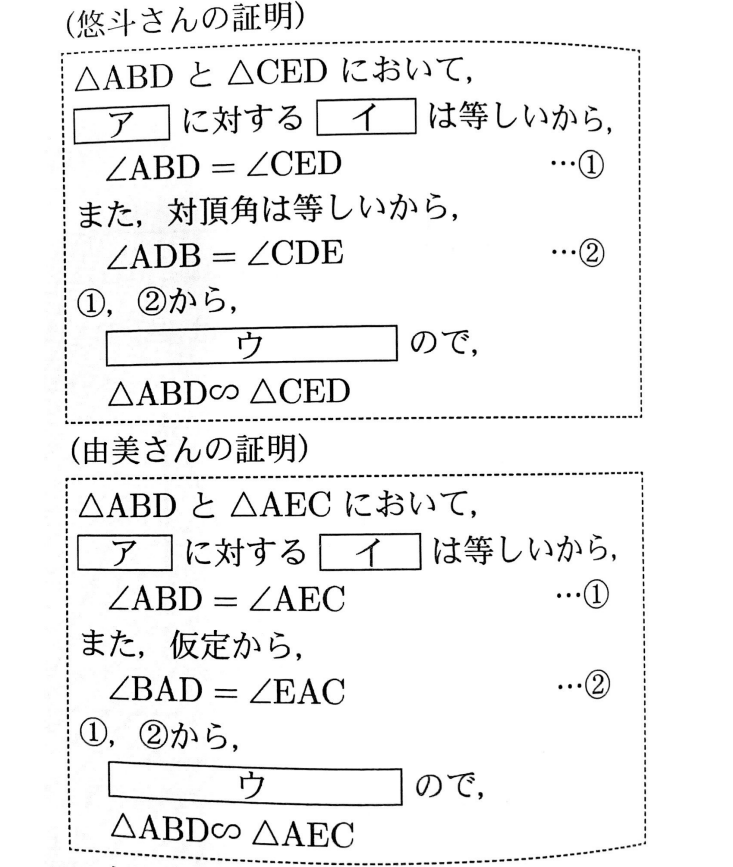
悠斗さんと由美さんは、コンピューターを使って、画面のように、線分ADを延長した直線と円Oとの交点をEとしました。次に、点A,B,Cを円周上で動かし、悠斗さんは「△ABDと△CEDが相似である」、由美さんは「△ABDと△AECが相似である」と予想し、それぞれ予想が成り立つことを証明しました。

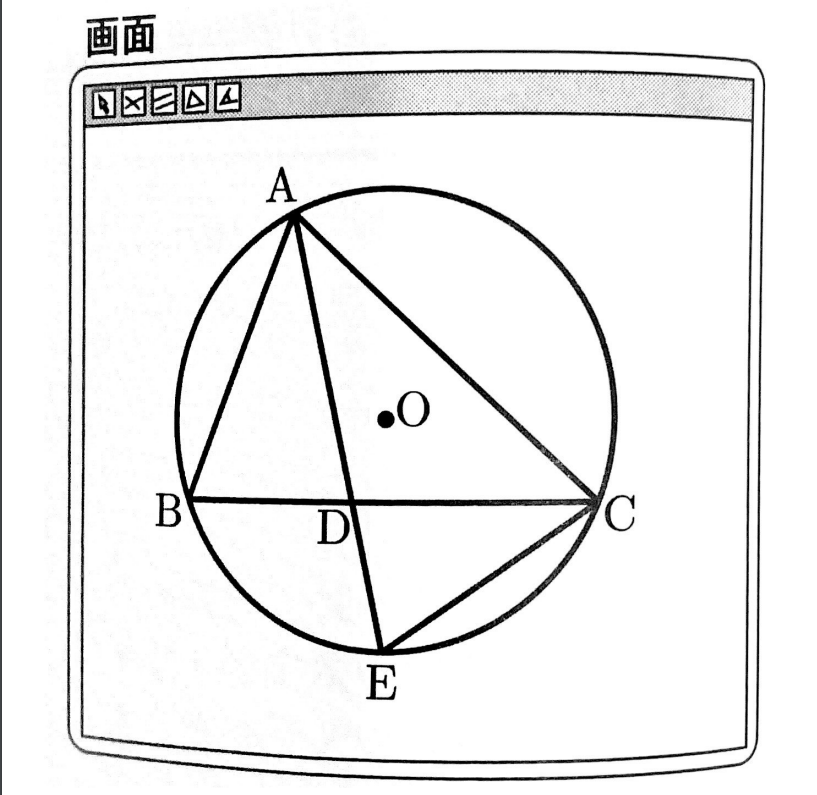
次の（1）（2）に答えなさい。
（1）＜ア＞～＜ウ＞には、それぞれ共通する言葉が入ります。＜ア＞～＜ウ＞に当てはまる言葉をそれぞれ書き入れ、証明を完成させなさい。
（2）AB＝ADのとき、△ABE≡△ADCを証明しなさい。なお、悠斗さんや由美さんが証明したことを用いてもよいものとします。

解答・解説

問1

∠ADC＝110°
AD＝CDより、△ADCは二等辺三角形なので∠DAC＝∠DCA、ADは∠BACの二等分線なので、∠BAD＝∠DAC＝35°
よって、∠ADC＝（180°－∠DAC－∠DCA）＝110°

問2

（1）＜ア＞弧AC　＜イ＞円周角　＜ウ＞二つの角の大きさがそれぞれ等しい
（2）解答・解説略
解説ご希望の方はお気軽にお問い合わせください。