

今回は、中学2年生の総復習、「総まとめテスト」をやっていきます。
是非、一緒に解いて、理解を深めていきましょう!
不安な方は各単元に戻って復習してから解くのをおすすめします。
(1)
2x²-x+6
-) x²-x-15
(2)2(a-3b)-(5a-b)
(3)4ab×(-2a)÷8ab
(4)3x+y/2-x-2y/3
(5)4x-{3x-2(x-6)-5}
(1)x²+21
ひくときは、ひく数の符号に注意!
(2)-3a-5b
2a-6b-5a+b=-3a-5b
答えに「-」を書き忘れないこと。
(3)-a
4ab×(-2a)/8ab=-8a²b/8ab=-a
(4)7x+7y/6
3x+y/2-x-2y/3
=3(3x+y)-2(x-2y)/6
=9x+3y-2x+4y/6
=7x+7y/6
(5)3x-7
4x-{3x-2(x-6)-5}
=4x-(3x-2x+12-5)=3x-7
(1)a=-2のとき、2a²+3aの値を求めなさい。
(2)a=3b+rをbについて解きなさい。
(3)S=1/2(a+b)hをaについて解きなさい。
(4)連立方程式ax+by=5,ax-by=-1の解が、x=2,y=-1であるとき、a,bの値を求めなさい。
(1)2
2×(-2)²+3×(-2)=1
(2)b=a-r/3
a=3b+r
3b+r=a
3b=a-r
b=a-r/3
(3)a=2S/h-b
(4)a=1,b=-3
x=2,y=-1を代入して、a,bの解を求めます。
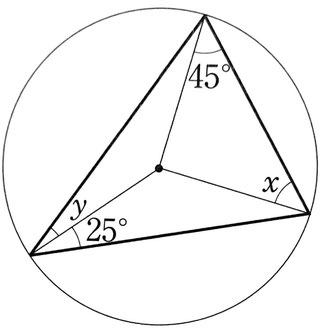
∠x=45°,∠y=20°
(1)
3x+2y=4
y=3x-7
(2)
2x-y=7
x+y=2
(3)5x-7y=2x-3y+5=7
(1)x=2,y=-1
(2)x=3,y=-1
(3)x=7,y=4
7を中心に連立方程式をつくる。
5x-7y=7
2x-3y+5=7
を解きます。
(1)八角形の内角の和を求めなさい。
(2)正十二角形の1つの内角は何度ですか。
(3)正n角形の1つの内角が135°のとき、対角線の総本数を求めなさい。
(1)1080°
n角形の内角の和は180°×(n-2)なので、
180°×(8-2)=1080°
(2)150°
1つのが外角は、360°÷12=30°
内角は、180°-30°=150°
(3)20本
内角が135°→外角は180°-135°=45°
360÷45=8 八角形
n角形の対角線の総本数は、n(n-3)/2本より、
8×(8-3)/2=20(本)
(1)xとyの関係を連立方程式で表すと、
【 ア 】=9
【 イ 】=1/2 となる
(2)2人がA地で出会うのは、午前【 ウ 】である。
(1)ア 10x+4y,イ y-x
アに入る式は、=9から考えて、距離の合計が9㎞ということになります。
→10x+4y=9
イに入る式は、=1/2から考えて、2人の進んでいる時間の差が1/2時間(30分)ということになります。
拓海さんの方が先に出発しているので、y-x=1/2になります。
(2)10時30分
方程式を解くと、x=1/2,y=1となるので、2人が出会う時期は、拓也さんが家を出発してから、1/2時間(30分)後の、10時30分になります。
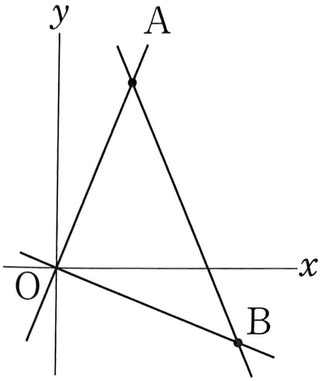
(1)直線ABの式を求めなさい。
(2)△AOBの面積を求めなさい。
(3)x軸上の正の部分に点Pをとって、△AOBの面積と、△AOPの面積が等しくなるようにしたい。このときの点Pの座標を求めなさい。
(1)y=-2x+8
2点A(2,4),B(5,-2)を通ることから、ax+b=yに代入して、連立方程式をつくり、aとbの値を求めます。
(2)12
「バッテン戦法」を使います。
4×5-2×(-2)/2=12
(3)(6,0)
△AOPの面積は、底辺がOP、高さが点Aのy座標だから、
OP×4×1/2=12よってOP=6
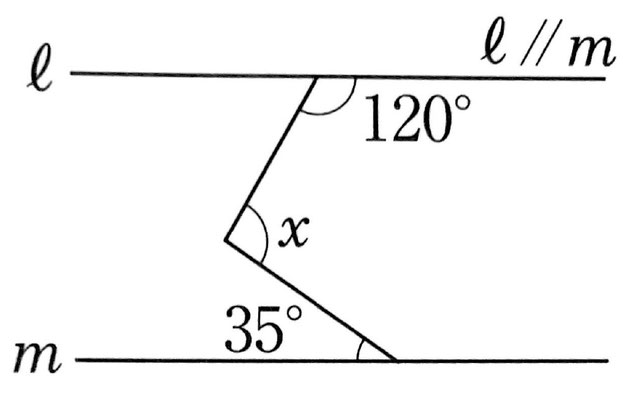
(1)
(2)
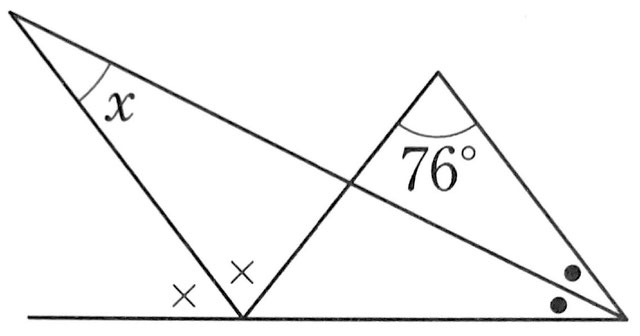
(1)95°
(2)38°
●●+76°=×× 両辺を1/2にすると
●+38°=×
●+∠x=× より、∠x=38°
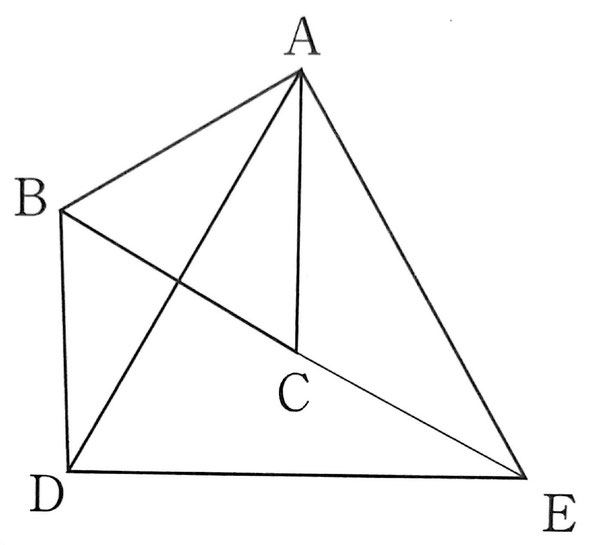
△ABDと△ACEにおいて、
AB=AC・・・①
AD=AE・・・②
∠BAD+∠DAC=60°
∠CAE+∠DAC=60°より、∠BAD=∠CAE・・・③
➀,②,③より、2辺とそのはさむ角が等しいので、
△ABD≡△ACE
よってBD=CE
(1)大小2つのさいころを投げたとき、目の数の和が3より大きくなる確率を求めなさい。
(2)赤玉3個、青玉2個はいっている袋があります。この袋から2個の玉を同時に取り出すとき、2個とも同じ色になる確率を求めなさい。
(1)11/12
目の数の和が2になるのは、1と1の1通り。
目の数の和が3になるのは、1と2,2と1の2通り。
大小2つのさいころを投げたときの目の出かたは、6×6=36(通り)
よって、目の数の和が3位かになる確率は、3/36
目の数の和が3より大きくなる確率は、1-3/36=11/12
(2)2/5
5個の玉の中から、2個を取り出す場合の数は、組み合わせなので、
5×4/2(個)=10(通り)
2個とも赤玉になる場合の数は、3個の中から2個を選ぶ組み合わせなので、
3×2/2(個)=3(通り)
2個とも青玉になる場合の数は1通り。
よって確率は4/10=2/5になります。
最後までご覧いただきありがとうございました!
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。
ひのきあすなろでは、無料の体験授業を実施しています。
ぜひ具体的な指導の様子を知る際に、ご活用ください!
体験授業の日程は相談頂けるので、忙しいお子さんにもぴったりです。
など、勉強に関するあらゆるお悩みをアドバイザーが解決致します!
家庭教師を検討している方、勉強に関するお悩みをお持ちの方、塾からの乗り換えを考えている方など、どんなお子さんもOK!
入会するかは、体験授業の後、じっくりとご家族でご相談いただければけっこうです。
まずは、お気軽に「無料の体験授業」で勉強に関する悩みについてアドバイスをうけてみませんか?
ひのきあすなろの指導では、勉強のやり方や習慣作りの指導から受験対策まで、お子さんの目標に合わせたカリキュラムを組んで指導をさせて頂いております。
ひのきあすなろが勧める勉強法は学年別・目的別に以下のページにて詳しくご案内させていただいています。
家庭教師のひのきあすなろでは、対面指導・オンライン指導の両方に対応しています。
対面での指導が難しい地域にお住まいの方や、感染症への感染リスク軽減などで対面指導が難しい場合などでも、指導を続けられる体制を整え、お子さんの学びがとまらないよう制度を整えて、指導を行っています。
家庭教師のひのきあすなろでは、無料の体験授業を実施しています。
小学生のお子さんには、一人で勉強する時の基本的な勉強の進め方や、予習復習のやり方など、勉強習慣を身に付け正しい勉強方法を身に付けていけるようなアドバイスをさせて頂きます。
小学生のお子さんは、まだまだ親御さんがサポートしてあげることが必要となることも多い年ごろです。お子さんが勉強面で悩んでいるようならば、試しに無料の体験授業にお申込み下さい。
体験授業では、指導豊富なスタッフがお子さんから今のお悩みや不安などを引き出し、解決に導いていきます。
