

こんにちは!夜に見ている人はこんばんは!家庭教師ひのきあすなろスタッフの百田(ももた)です。
今回から相似な図形について解説をしていきたいと思います!今までの計算系の問題とは種が変わって、図形問題が主になります。そして相似はめちゃくちゃ大事です。入試問題には絶対に出てきます。相似を制すものは図形を制します。そのレベルの単元です。
改めまして、今回のターゲットは「相似な図形」です。前述の通り大事な単元なので、大増量の全8回でお送りしていきたいと思います。
第一回目の今回は相似な図形とは何ぞやといったところから解説していきたいと思います。
形式としては1・2回目と5・6回目の基礎編で基本を学んでいき、3・4回目と7・8回目は実践編に移っていきますので、是非最後までお付き合いください!
文部科学省 学習指導要領「生きる力」
http://www.mext.go.jp/a_menu/shotou/new-cs/index.htm
さて、早速やっていきましょう!
図形は今まで中学校1年生からやってきましたね。平面図形と空間図形。
中学校2年生では合同な図形について学びました。
中学校3年生では相似な図形について学んでいきます。これは小問集合から証明問題までバリエーション豊かに入試問題に登場します。凄く大事な単元です。僕もお母さんからよく言われました。「しっかり掃除(相似)やっておきなさい!」と。
冗談はさておき、相似とは何かを学んでいく前に、中学校2年生で行った合同に関して少し復習をしながら、違いを見比べていきましょう。
合同は「全く同じ形」の図形でした。記号は「≡」を使いましたね。
今回の相似は「少し似ている形」を探していきます。記号は「∽」というものを使います。Sを横にした形です。
合同よりも相似の方が少し似ているだけで条件クリアなのでたくさんあります。
魚だと”スズキ”と”シーバス”は呼び方が違うだけで、同じ魚の合同だけど、”ヤマメ”と”アマゴ”は違う魚だけど、同じ淡水の渓流魚だから相似だねって感じです。
図形の話に戻ると、重ねたときにピッタリと重なるものが合同な図形、拡大や縮小されているものが相似な図形です。
さて、問題を解いていきましょう。
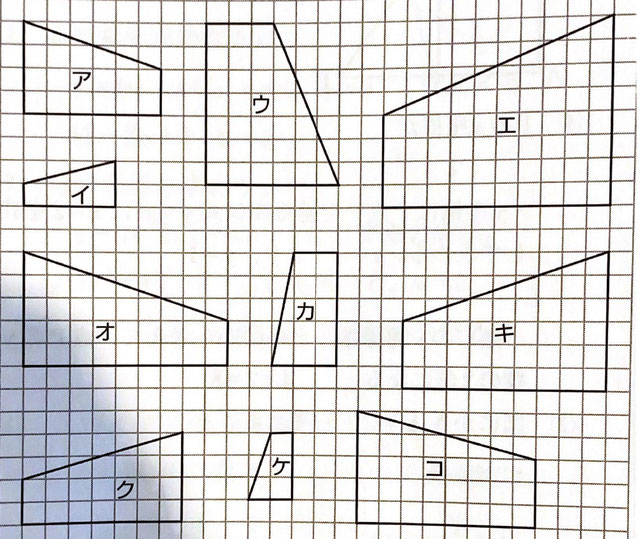
さて、見ていきましょう。
まずアの四角形左上の角から便宜上、時計回りにABCDとすると、ADがマス4つ、CDが6つ、BCが2つ、ABが縦2つ横6つです。
順に見ていきましょう。
イを反転させて、アと同じような形にします。同じ様にを振ると、ADがマス2つ、CDが4つ、BCが1つ、ABが縦2つ横4つです。
ADとCDに注目しましょう。ADの長さが1/2になっているので、縮小されていれば、CDは3マスになるはずです。しかし、イは4マスなので、アとイは相似ではありません。
ココからは短縮していきます。
ウはADが6マス、CDが7マス。拡大ならば3/2倍になるはずですが、不適。
エはADが8マス、CDが10マス。拡大ならば2倍になるはずですが、不適。
オはADが5マス、CDが9マス。拡大ならば5/4倍になるはずですが、不適。
カはADが3マス、CDが5マス。縮小ならば3/4倍になるはずですが、不適。
キはADが6マス、CDが9マス。拡大ならば3/2倍になるはずです。6×3/2=9。ついに一つ目を見つけました!!念のために他の辺も見てみましょう。BCは2×3/2=3になって欲しいです。見てみると、確かに3マス!ABも問題ありません。第一相似発見です!!
クはADが4マス、CDが7マス。すぐに違うことが分かりますね。
ケはADが2マス、CDが3マス。縮小ならば1/2倍になるはずです。6×1/2=3。これも相似ですね!二つ目を発見です。
コはADが5マス、CDが8マス。拡大ならば5/4倍になるはずですが、不適。
よって、アと相似な図形はキとケの二つだということが分かります。
次の要点です。相似比です。
これは読んで字のごとく。相似な図形の拡大や縮小の比率の事です。
例えば、例題1ならば、アとキの相似比は2:3になり、アとケの相似比は2:1ということになります。
この相似比が分かることで一方の辺の長さが分かれば、他方の辺の長さも知ることができます。
いわば「相似相愛(本当の言葉は”相思相愛”です)」な関係ですね。
失敬、問題を解いていきましょう。
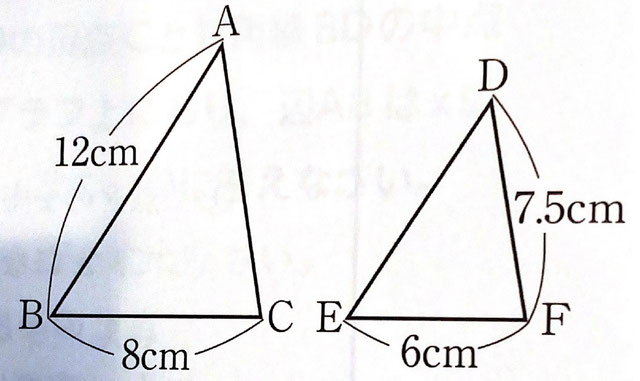
合同な図形のときもそうでしたが、問題文に○∽△と書いてあった場合はチャンスです。数学のルールとして対応する順番に書かないといけないというルールがあるので、対応する角や辺がすぐ分かります。
今回は△ABC∽△DEFなので、ABとDE、BCとEF、CAとFDが対応しているということが分かります。
設問に入っていきましょう。
(1)△ABCと△DEFの相似比を求めなさい。
両方長さの分かっている、BCとEFに注目しましょう。
BC:EF=8cm:6cm=4:3
が答えとなります。
(2)辺DEの長さを求めなさい。
ここからが相似の本領発揮です。年末の大掃除(相似)です。
辺DEと対応をしているのは辺ABです。よって、
AB:DE=12cm:DE=4:3【相似比】
⇔4DE=3×12
⇔DE=9cm
このように求めることができます。
(3)辺ACの長さを求めなさい。
前問と同様にやっていきましょう。
辺ACと対応をしているのは辺DFです。よって、
AC:DF=AC:7.5cm=4:3【相似比】
⇔3AC=4×7.5
⇔AC=10cm
と求めることができます。
いかがでしたでしょうか??
このような感じで8回の記事を読めば、君も相似な図形マスターにきっとなることができるでしょう。
大事なのは「意外と簡単だ!」とか「分かると面白い!」と感じることです。数学だけでなく、全ての教科に精通します。
ひのきあすなろでは体験授業で勉強のコツを教えていますので、この機会に是非お試しください!!
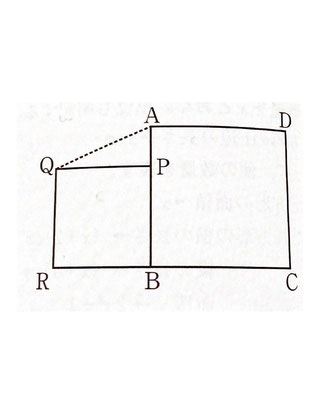
今回の二次方程式の利用の中で一番難易度の高い問題です。順を追ってやっていきます。
まず、問題文よりPQ=x【cm】が与えられます。BPQRは正方形なので、RB=x【cm】・・・①であることも分かります。
次に、CR=8cmより、①を使うことによってBCの長さが表せます。BC=CR-RB=8-x【cm】です。さらにABCDも正方形なので、AB=8-x【cm】・・・②となります。
そして、△AQPの面積が3cm²から、APが逆算できます。PQ(=x)×AP÷2=3より、AP=6/x【cm】・・・③となります。
ここで、AB=AP+PBに注目すると、方程式が作れます。
PB=PQ=x【cm】・・・④なので、②~④より、
8-x=6/x+xという式が成り立ちます。
これを解いていきましょう。
x(8-x)=6+x²
⇔2x²-8x+6=0
⇔x²-4x+3=0
⇔(x-1)(x-3)=0
⇔x=1,3
PB>PAより、PQ=3cm
以上で二次方程式の利用の解説記事を終了します。少しはお役にたてましたか??解説記事は随時上げていくので、またよければお付き合いください。
全4回の内容、お疲れ様でした。二次方程式の利用マスターになれましたか??
大事なのは「意外と簡単だ!」とか「分かると面白い!」と感じることです。数学だけでなく、全ての教科に精通します。
ひのきあすなろでは体験授業で勉強のコツを教えていますので、この機会に是非お試しください!!
ひのきあすなろでは、ご希望のお子さんに対して無料の体験授業を実施しています。
具体的な授業内容や先生たちの指導の様子を知る際に、ぜひご活用ください!
体験授業の日程は相談頂けるので、忙しいお子さんにもぴったりです。
など、勉強に関するあらゆるお悩みをアドバイザーが解決致します!
家庭教師を検討している方、勉強に関するお悩みをお持ちの方、塾からの乗り換えを考えている方など、どんなお子さんでもOK!
入会するかは、体験授業の後じっくりとご家族でご相談いただければけっこうです。
まずは、お気軽に「無料の体験授業」で勉強に関する悩みについてアドバイスを受けてみませんか?
いつでもお問い合わせをお待ちしております!
ひのきあすなろの指導では、勉強のやり方や習慣作りの指導から受験対策まで、お子さんの目標に合わせたカリキュラムを組んで指導をさせて頂いております。
ひのきあすなろが勧める勉強法は学年別・目的別に以下のページにて詳しくご案内させていただいています。
家庭教師のひのきあすなろでは、対面指導・オンライン指導の両方に対応しています。
対面での指導が難しい地域にお住まいの方や、感染症への感染リスク軽減などで対面指導が難しい場合などでも、指導を続けられる体制を整え、お子さんの学びがとまらないよう制度を整えて、指導を行っています。
家庭教師のひのきあすなろでは、無料の体験授業を実施しています。
小学生のお子さんには、一人で勉強する時の基本的な勉強の進め方や、予習復習のやり方など、勉強習慣を身に付け正しい勉強方法を身に付けていけるようなアドバイスをさせて頂きます。
小学生のお子さんは、まだまだ親御さんがサポートしてあげることが必要となることも多い年ごろです。お子さんが勉強面で悩んでいるようならば、試しに無料の体験授業にお申込み下さい。
体験授業では、指導豊富なスタッフがお子さんから今のお悩みや不安などを引き出し、解決に導いていきます。
